This year FIBA launched a new European professional competition for basketball clubs, namely, Basketball Champions League (BCL). A total of 52 teams from 31 European leagues participated in the inaugural season of BCL and the actual format of the competition can be found on the league’s site. Currently the competition is at the first round of playoffs. In contrast to the NBA, each playoff round includes two games. Each team of the matchup will have one home game, with the team with home advantage playing the second game at this home court. The team that has the best aggregate point differential between the two games qualifies to the next round.
Currently there are 24 teams left into the competition. 8 of them have qualified to the top-16 round directly from the group stages. Hence, the first playoff round includes 16 teams from which 8 teams will qualify to the next round. Consquently we will have the round of 16, the quarter final round and at the end the final four!
In a previous post I introduced the BPM model that can provide win probabilities for a given basketball matchup. However, this is not enough for the format of BCL. We need a model that provides the expected point differential of a matchup. Then by estimating through repeated simulations the distribution of the point differential for the two games of the round we can provide a probability of advancing to the next round for each team. The independent variables of the model are still the same as in BPM. However the independent variable is not a categorical one representing W-L but rather a continous one representing the point differential of the result. BCL is providing the advanced statistics that our model requires as input (other Euro(pean)-leagues 🙂 do not). However, they are not provided on a per-game basis but rather average statistics for each team. Therefore, the resampling module of BPM engine cannot be used directly. However, using the provided data we estimate the variance over the league for each feature and for every team we use this variance and the corresponding mean of the feature to sample a value for each simulation. Simply put we make the (not-necessarily true) assumption that the variance of the performance is constant across the teams of the league. When simulating each pair of matchups we will obtain a distribution for the aggregate point differential. This distribution will provide us with the corresponding advancement probabilities. For example, simulating 10,000 the matchup between AEK Athens and Juventus we have the following distribution.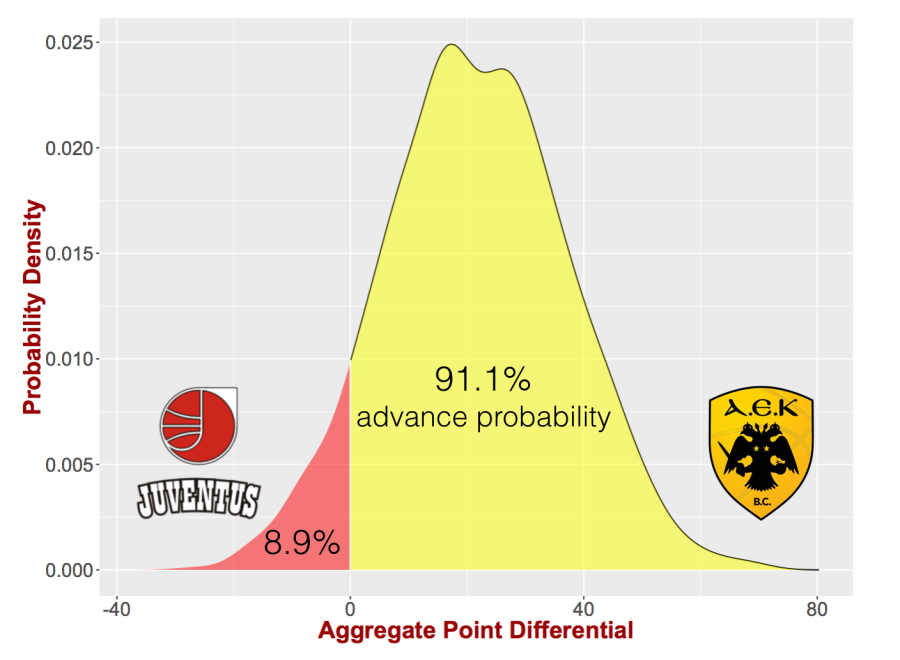
In 91.1% of the simulations AEK advances since it has the better aggregate point differential. Following we start by presenting the projected probabilities of advancement for the play-offs qualifiers and later we will update the probabilities for the whole tournament once the round of 16 matchups are known.
Play-offs Qualifiers
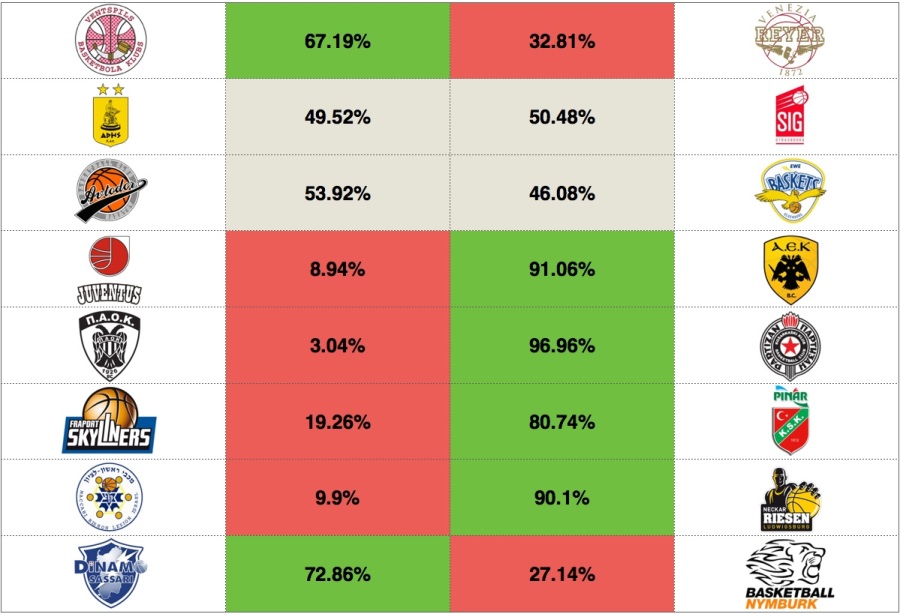
[2/16/2017] Considering the results from the first leg of the qualifiers we obtain the following advancement probabilities.
As we can see there is not any real close matchup. Aris and Avdotor Saratov took a clear advantage from the first game even though prior to the first game there was not a team with a clear advantage at the corresponding matchups. Furthermore, Fraport Skyliners slightly increased their chances of advancing, but they are still the underdog in their matchup with Pinar Karsiyaka. Overall, this playoff round seems to be very unbalanced.
[2/23/2017] Top-16 Play-offs round
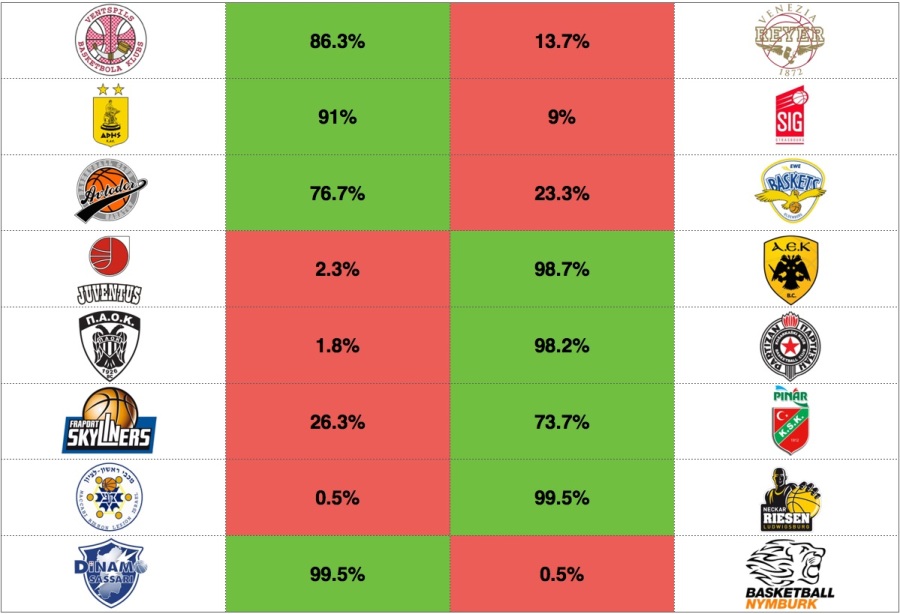
With the qualifier round over (and having a 5-3 prediction record – not good, but right around the state-of-the-art of prediction models) and the next play-off round set, it is time to make our next predictions, that is, what are the chances of each team qualifying to the quarter finals of the league. One of the problems with the model is the variance with regards to the model features. In order to overcome this problem we first used the variance across all the teams for each features. However, this provides very small variance for each feature, which results in effectively estimating the probability of winning based on purely the average of each feature. For that purpose, we included a 5% variance for each of the features in order to add an appropriate randomization component in the simulations. Note, that if the league provided us with individual game data, we would be able to calculate the actual variance of the performance for *each* team. We could even potentially identify what the variance is when the team has played in the past with other teams that are similar to the upcoming opponent. For example, we see that AEK is projected with an 85.3% probability of advancing to the quarter-finals. However, this is largely due to the fact that our data cannot account for the fact that AS Monaco is the best defense in the league. I would expect the actual probability to be lower (around the 60%-65%). Also another interesting point is that PAOK is projected only with a 5.5% probability of advancing. PAOK had an even lower probability against Partizan and managed to advance. It must be the case that PAOK has a lot of intangibles that cannot be modeled by the four factors model.
[3/2/2017] Top-16 Play-offs round – leg 2
Updated probabilities after the first leg of the qualifiers.
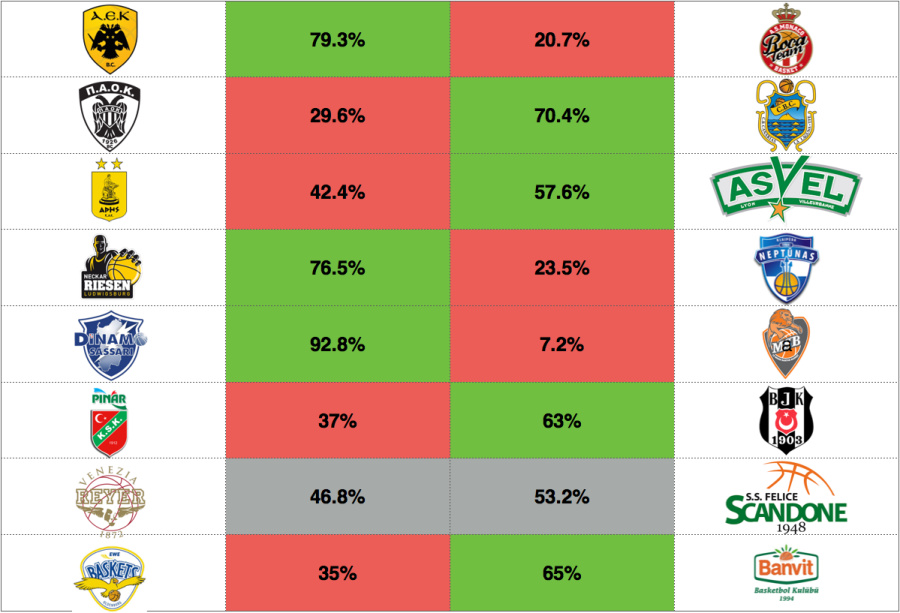
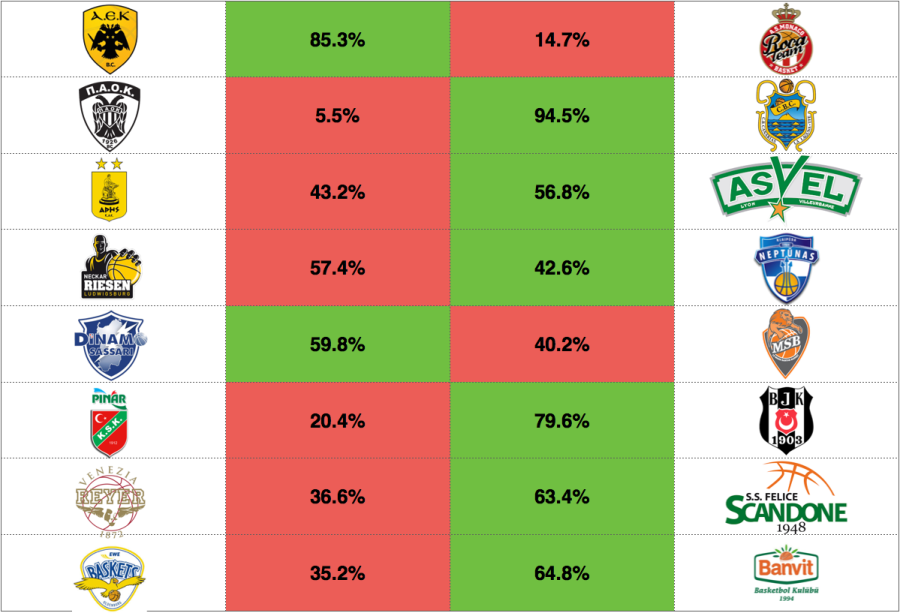
[3/12/2017] Top-8 Play-offs round – leg 1
Here are the predictions for the last step before the final four. Some close match-ups and some that look more skewed. Until now our model has a 66% accuracy in predicting the advancing teams. Following are the final-4 probabilities before leg 1:
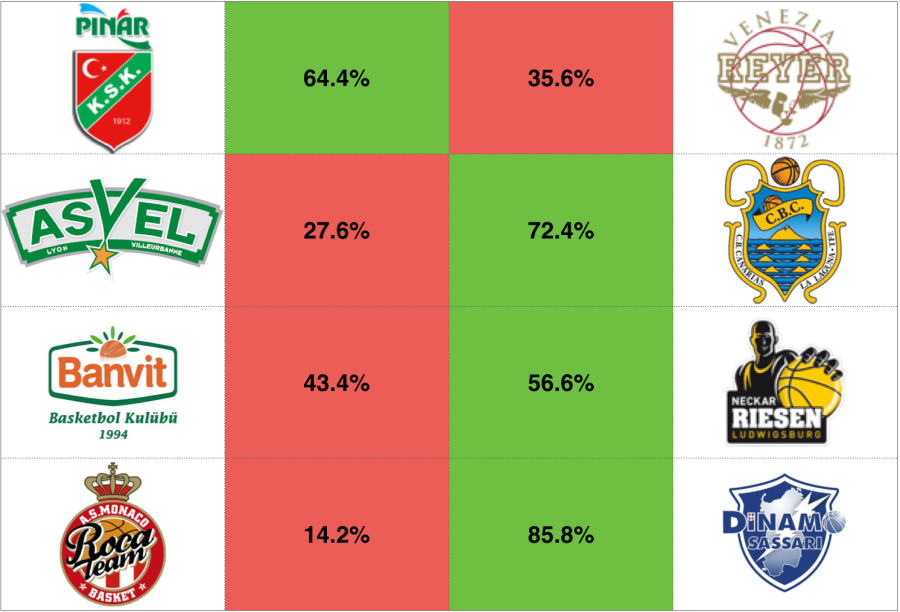
The big change after the first leg is at the Monaco-Sassaro matchup, where the 11 point win for the French team pretty much brought the advancement to the final four to pretty much a coin-toss.
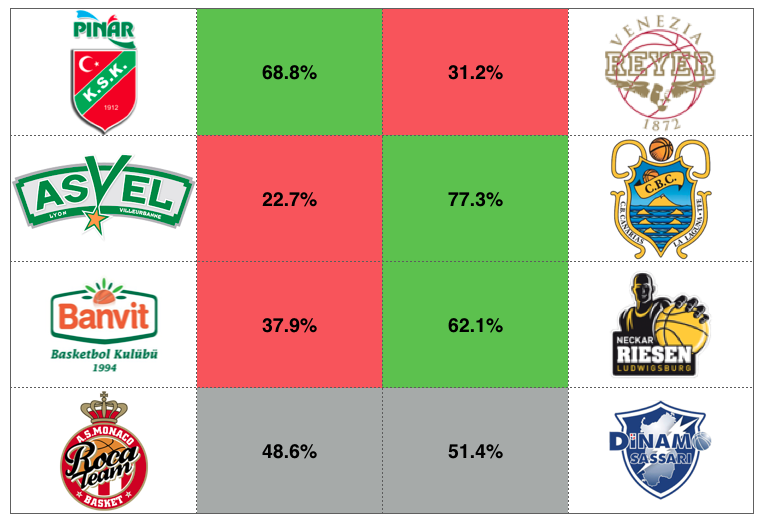
[4/6/2017]Final four
It is the time for the big dance of the first edition of the Basketball Champions League and it seems that there is a big favorite and this is no other than the host of the final four, Iberostar Tenerife.
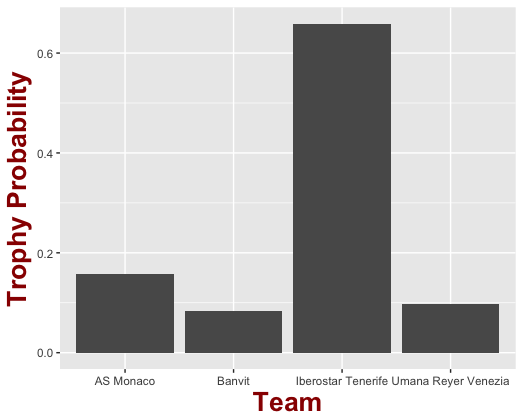
Regardless of what math say, this is set to be a fascinating tournament!

[…] via Predicting the Basketball Champions League Tournament using Data — The Athlytics Blog […]
LikeLike